SHA1加密算法

发表于： 2026-01-20 分类于：密码学与安全

字数： 2257 阅读：≈ 5分钟浏览：评论：

SHA1 算法和 MD5 总体上很类似,算法流程也差不多

原始数据准备

还是以"password"这个字符串的数据为例
转换成十六进制就是: 70 61 73 73 77 6f 72 64,长度 8 个字节,64 位
接下来开始填充,先补一个 1,再补 k 个 0,使得消息满足 ()64+1+k) = 448
64+1+k = 448 即 k=383,需要补一个 1 和 383 个 0
最后 64 位用来表示原始数据的长度,原始数据长度为 8 个字节,64 位,用 0x0000000000000040(16 进制,大端序)
SHA-1 使用大端序,所以这 8 个字节直接按照顺序附加

填充完成,如下所示:

1
2
3
4
70 61 73 73 77 6f 72 64 80 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 40

消息扩展

这里是另一个与 MD5 不同的地方
目标:将一个 512 位,16 个 32 位(字)的数据段,扩展成 80 个 32 位(字)的数据段(w[0]~w[79]),用于后续的 80 步压缩算法

第一步:初始化 16 个字这 16 个字来自于 512 位的数据段,SHA-1 使用大端序,所以每个 32 位字由 4 个连续的字节构成
数据块:B0,B1,B2,B3,B4…..B63(每个 B 是一个字节)

w[0] = (B0<<24)|(B1<<16)|(B2<<8)|B3
w[1] = (B4<<24)|(B5<<16)|(B6<<8)|B7
……
w[15] = (B60<<24)|(B61<<16)|(B62<<8)|B63 对于字符串"password",填充过后的 16 个字就应该是:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
W[0]  = 0x70617373
W[1]  = 0x776f7264
W[2]  = 0x80000000
W[3]  = 0x00000000
W[4]  = 0x00000000
W[5]  = 0x00000000
W[6]  = 0x00000000
W[7]  = 0x00000000
W[8]  = 0x00000000
W[9]  = 0x00000000
W[10] = 0x00000000
W[11] = 0x00000000
W[12] = 0x00000000
W[13] = 0x00000000
W[14] = 0x00000000
W[15] = 0x00000040

第二步:扩展后 64 个字(w[16]~w[79])
这个是扩展的核心部分,对于 t 从 16 到 79,每一个 w[t] 都是由前面已有的 4 个值通过异或和循环左移得到的
计算公式: W[t] = ROTL^1(W[t-3] XOR W[t-8] XOR W[t-14] XOR W[t-16] )

ROTL^1(x) 代表将 x 循环左移 1 位
XOR:按位异或的操作下面来手动计算几个后面的值:
计算 w[16]:
w[16-3]=w[13]=0x00000000
w[16-8]=w[8]=0x00000000
w[16-14]=w[2]=0x80000000
w[16-16]=w[0]=0x70617373 接着,进行异或 0x00000000^0x00000000^0x80000000^0x70617373=0xF0617373
接着,循环左移 1 位, 0xF0617373的二进制是:1111 0000 0110 0001 0111 0011 0111 0011,左移 1 位得到 1110 0000 1100 0010 1110 0110 1110 0111
得到 w[16]=0xE0C2E6E7
再来算一下 w[17]
w[17-3]=w[14]=0x00000000
w[17-8]=w[9]=0x00000000
w[17-14]=w[3]=0x00000000
w[17-16]=w[1]=0x776f7264 异或: 0x00000000^0x00000000^0x00000000^0x776f7264=0x776f7264
0x776f7264=>0111 0111 0110 1111 0111 0010 0110 0100
左移 1 位: 1110 1110 1101 1110 1110 0100 1100 1000 得到 w[17]=0xEEDEE4C8
最后得到的 80 个字的数据块为:

1
['0x70617373', '0x776f7264', '0x80000000', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x0', '0x40', '0xe0c2e6e7', '0xeedee4c8', '0x81', '0xc185cdcf', '0xddbdc991', '0x102', '0x830b9b9f', '0xbb7b93a3', '0xc185cfcb', '0xdbaafeae', '0x76f72645', '0x408', '0xc2e6e7e', '0xedee4e0e', '0xc792f2e0', '0xb31632aa', '0x9952cf47', '0x66c64a92', '0x30b9bbfe', '0xb1ae0f04', '0x68bcedc4', '0xcc58cea2', '0x69655360', '0x76f764c7', '0xc4f1d0d7', '0xa813c6a9', '0x792f2e04', '0x31632bab', '0x16276fe6', '0xd71f3805', '0xd8c8ad8', '0x6a00e633', '0x740b38d7', '0xe5ee13ce', '0x96553c1a', '0x713da5b4', '0xe4218519', '0xf7cb5cf5', '0xa24b59b7', '0xa18b8288', '0x7c3d35e2', '0xbdab4ef7', '0xb1adfee0', '0xd6f907f1', '0x84425da0', '0xf6f2f847', '0x1a6bd892', '0x544e55ab', '0xd12392d0', '0x6626403e', '0x2f2e2491', '0x258d8c1', '0x481d8261', '0x1f380557', '0x8c8ad80d', '0xe6376a', '0x716b90a', '0x3fda26b', '0x344f6176', '0x4a8b3cfa', '0xab934a71', '0x1397939b', '0x1a935d6a', '0x323ad11d']

初始化常量

这里与 MD5 不同的是,它有 5 个初始化常量(A,B,C,D,E),初始值为固定的魔术常量(大端序)

1
2
3
4
5
6
7
h = [
	0x67452301,
	0xEFCDAB89,
	0x98BADCFE,
	0x10325476,
	0xC3D2E1F0
]

这些初始值将在处理完每个 512 位数据块后,与该块计算出的中间哈希值进行累加

处理分组数据

SHA1 跟 MD5 一样,都会涉及到 4 轮运算,每一轮扩展到 20 次,一共变成 80 次非线性函数的运算
首先来看一下 4 个非线性函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
for i in range(80):
    if 0 <= i <= 19:
        f = (b & c) | ((~b) & d)  # Ch(b, c, d): 选择函数
        k = 0x5A827999
    elif 20 <= i <= 39:
        f = b ^ c ^ d             # Parity(b, c, d): 奇偶校验函数
        k = 0x6ED9EBA1
    elif 40 <= i <= 59:
        f = (b & c) | (b & d) | (c & d) # Maj(b, c, d): 多数函数
        k = 0x8F1BBCDC
    else:  # 60 <= i <= 79
        f = b ^ c ^ d             # Parity(b, c, d)
        k = 0xCA62C1D6

80 次非线性运算被均分为 4 个阶段,每 20 步为一组,每个阶段使用不同的逻辑函数 f 和常量 k

接着来到具体的运算:

1
2
temp = ((a << 5) & 0xffffffff) | (a >> 27)  # 循环左移 5 位
temp = (temp + f + e + k + w[i]) & 0xffffffff

((a << 5) & 0xffffffff) | (a >> 27),这个实现了 32 位循环左移 5 位

a << 5:将 a 左移 5 位,但是右边移出的位会确实,自动补 0
a >> 27:将 a 右移 27 位,右移 27 位之后得到的正式原始 a 最左边的 5 位,现在位于结果的右侧了
|:按位或操作,将左移的 5 位与右移的 27 位合并,效果正好是将 a 循环左移了 5 位
& 0xffffffff:确保结果仍然是 32 位 temp = (temp + f + e + k + w[i]) & 0xffffffff:将所有的这个玩意儿混合到了一起
temp:循环左移 5 位过后的 a
f:上面的这个非线性函数
e:之前的那个初始化常量值
k:上面的常量 k 值
w[i]:填充过后的数据块的值

1
2
3
4
5
e = d
d = c
c = ((b << 30) & 0xffffffff) | (b >> 2)  # 循环左移 30 位
b = a
a = temp

算出来的值按照这样的规则进行交换如下图所示: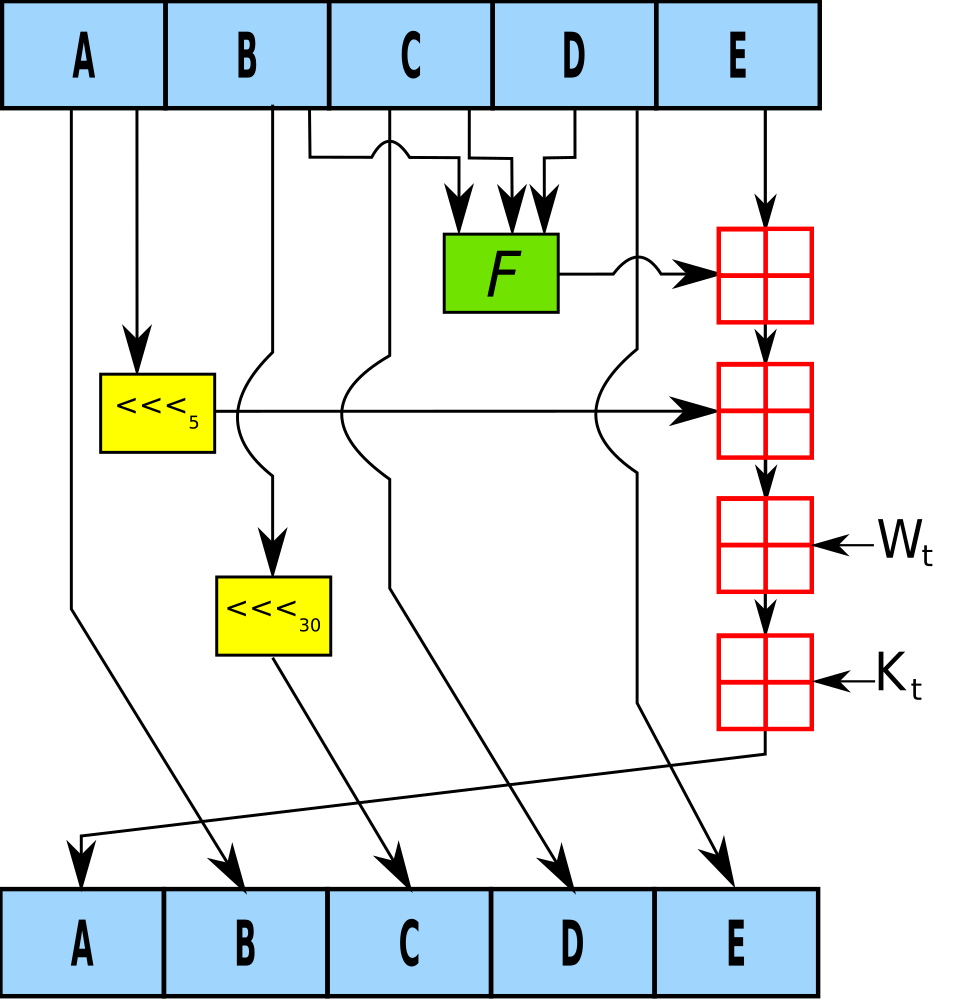

运算之后,a,b,c,d,e 值获得了更新,然后相加赋值给了 A,B,C,D,E,最后拼接起来,就得到了最终的值

python 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
def sha1(message: str) -> str:
    """
    计算输入字符串的 SHA-1 哈希值（40位十六进制小写字符串）
    """
    # === 步骤 1：预处理 ===
    
    # 转为字节（UTF-8）
    if isinstance(message, str):
        message = message.encode('utf-8')
    
    original_bit_len = len(message) * 8

    # 添加 bit '1'
    message += b'\x80'

    # 补零，直到长度 ≡ 448 (mod 512)
    while (len(message) * 8) % 512 != 448:
        message += b'\x00'

    # 添加 64-bit 原始长度（**大端序**）
    message += original_bit_len.to_bytes(8, 'big')

    # === 步骤 2：初始化哈希值（H₀）===
    h = [
        0x67452301,
        0xEFCDAB89,
        0x98BADCFE,
        0x10325476,
        0xC3D2E1F0
    ]

    # === 步骤 3：主循环（每 512-bit 一块）===
    for chunk_start in range(0, len(message), 64):  # 64 bytes = 512 bits
        chunk = message[chunk_start:chunk_start + 64]
        print("chunk:", chunk)
        # 将 chunk 拆分为 16 个 32-bit word（大端序）
        w = [0] * 80
        for i in range(16):
            w[i] = int.from_bytes(chunk[i*4:(i+1)*4], 'big')
        
        # 扩展到 80 个 word
        for i in range(16, 80):
            # SHA-1 使用循环左移 1 位
            w[i] = ((w[i-3] ^ w[i-8] ^ w[i-14] ^ w[i-16]) << 1) & 0xffffffff
            w[i] |= (w[i-3] ^ w[i-8] ^ w[i-14] ^ w[i-16]) >> 31  # 处理溢出位
        
        print("w:", [hex(w[i]) for i in range(80)])
        # 初始化工作变量
        print(h)
        a, b, c, d, e = h

        # 主压缩循环（80 步，分 4 轮）
        for i in range(80):
            if 0 <= i <= 19:
                f = (b & c) | ((~b) & d)
                k = 0x5A827999
            elif 20 <= i <= 39:
                f = b ^ c ^ d
                k = 0x6ED9EBA1
            elif 40 <= i <= 59:
                f = (b & c) | (b & d) | (c & d)
                k = 0x8F1BBCDC
            else:  # 60 <= i <= 79
                f = b ^ c ^ d
                k = 0xCA62C1D6

            temp = ((a << 5) & 0xffffffff) | (a >> 27)  # 循环左移 5 位
            temp = (temp + f + e + k + w[i]) & 0xffffffff
            e = d
            d = c
            c = ((b << 30) & 0xffffffff) | (b >> 2)  # 循环左移 30 位
            b = a
            a = temp

        # 更新哈希值
        h[0] = (h[0] + a) & 0xffffffff
        h[1] = (h[1] + b) & 0xffffffff
        h[2] = (h[2] + c) & 0xffffffff
        h[3] = (h[3] + d) & 0xffffffff
        h[4] = (h[4] + e) & 0xffffffff

    # === 步骤 4：输出最终哈希值（十六进制小写）===
    return ''.join(f'{val:08x}' for val in h)


# === 测试 ===
if __name__ == "__main__":
    msg = "password"
    print(sha1(msg))

常见的魔改点

初始化常量
非线性函数逻辑
k 值
……